Senin, 15 April 2019
Manipulasi Date SQL Server
CAST(CAST(year(golivedate) AS varchar) + '-' + CAST(month(golivedate) AS varchar) + '-' + CAST(1 AS varchar) AS DATETIME) as period
Selasa, 09 April 2019
Hubungan Jenis Kelamin dengan Total Belanja dengan t.test
Berdasarkan kasus diatas kita akan melihat hubungan antara data kategorik dan numerik, yaitu variabel jenis kelamin dan total belanja. Sebelum menguji hubungannya, sebaiknya dilihat perbedaan rata-rata total belanja untuk laki-laki dan perempuan dengan visualisasi yaitu menggunakan boxplot. Boxplot grafik statistik dari data dengan komponen lima ukuran statistik yaitu Min, Q1,Q2, Q3, dan Max. Untuk lebih jelasnya mengenai boxplot dapat dilihat gambar dibawah ini
Selanjutnya analisis inferensia yaitu untuk mengetahui apakah ada perbedaan rata-rata total belanja pada laki-laki dan perempuan maka digunakan statistik uji t-test.
Untuk melakukan visualisasi boxplot dan uji statistik t-test pada R tahapannya sebagai berikut
boxplot(Total~Jenis.Kelamin,data = data_intro)
t.test(Total~Jenis.Kelamin,data = data_intro)
t.test(Total~Jenis.Kelamin,data = data_intro)
Function boxplot digunakan untuk melihat secara grafik rata-rata total belanja pada laki-laki dan perempuan, sedangkan perintah t.test digunakan untuk melihat hubungan secara statistik. Penggunaan kedua fungsi diatas yaitu variabel pertama yang bertipe numerik, sedangkan variabel kedua variabel kategorik. Hipotesis t-test sebagai berikut :
- Null hipotesis : tidak ada perbedaan rata-rata total belanja antara laki-laki dan perempuan
- Hipotesis alternatif : ada perbedaan rata-rata total belanja antara laki-laki dan perempuan
Hubungan Produk dengan Tingkat Kepuasan dengan chisq.test
Berdasarkan kasus diatas kita akan melihat hubungan antara data kategorik dan kategorik, yaitu variabel jenis produk dan tingkat kepuasan. Sebelum menguji hubungannya, sebaiknya dilakukan tabulasi silang sebagai analisis deskriptif. Selanjutnya analisis inferensia yaitu menguji apakah ada hubungan maka dapat digunakan chi-square test.
Untuk melakukan tabulasi dan uji statistik chi-square test pada R tahapannya sebagai berikut
table(data_intro$Produk,data_intro$Tingkat.Kepuasan)
chisq.test(table(data_intro$Produk,data_intro$Tingkat.Kepuasan))
chisq.test(table(data_intro$Produk,data_intro$Tingkat.Kepuasan))
Perintah table untuk melihat tabulasi antar variabel kategorik, sedangkan perintah chisq.test digunakan untuk melihat hubungan secara statistik.
Hubungan Pendapatan dengan Total Belanja dengan cor.test
Setelah melihat hubungan variabel pendapatan dengan total belanja menggunakan scatter plot diatas maka kita akan mengujinya, apakah benar-benar pendapatan memiliki pengaruh positif terhadap total belanja
Untuk melakukan uji korelasi pada R menggunakan perintah
cor.test(data_intro$Pendapatan,data_intro$Total)
Berikut penjelasan function diatas:
- Function cor.test digunakan untuk melihat hubungan secara statistik.
- Pada korelasi test untuk mengujinya kita memakai t-test. Dengan hipotesis sebagai berikut:
- H0 : tidak ada hubungan antara pendapatan dan total belanja.
- Ha : terdapat hubungan antara pendapatan dan total belanja
Tugas Praktek
Lengkapi bagian [...1...] pada code editor untuk seperti yang ada pada bagian Lesson.
Jika berhasil maka keluaran akan sebagai berikut.
> cor.test(data_intro$Pendapatan,data_intro$Total)
Pearson's product-moment correlation
data: data_intro$Pendapatan and data_intro$Total
t = 3.1168, df = 18, p-value = 0.005957
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2026033 0.8197871
sample estimates:
cor
0.5920437
Refresh Dasar Statistik
Hipotesis : https://www.slideshare.net/rhandyprasetyo/statistikauji-hipotesis
Korelasi : https://dsmlmdblog.blogspot.com/2016/03/pengertian-dan-perhitungan-korelasi.html
Korelasi : https://dsmlmdblog.blogspot.com/2016/03/pengertian-dan-perhitungan-korelasi.html
Pengertian dan Perhitungan Korelasi Pearson Product Moment
Dalam penelitian tertentu, terkadang kita perlu mengetahui bagaimana hubungan antara objek yang kita amati dengan objek yang lainnya. Untuk mengetahui hubungan tersebut, dapat dilakukan analisis korelasi. Dalam postingan saya kali ini, saya akan membahas mengenai pengertian, cara, dan analisis perhitungan korelasi. Bagian kali ini yang akan saya bahas yaitu mengenai analisis korelasi linear sederhana atau biasa disebut dengan simple linear correlation atau Pearson product moment correlation.
Pada umumnya, korelasi berasal dari dua kata, yaitu "Co-" dan "Relation". Kata "Co-" menunjukkan bersama, bergabung, sepasang, atau derajat/tingkat yang sama. Dan "relation" menunjukkan relasi, dampak atau hubungan. Jadi secara umum, definisi korelasi menurut penggunaan statistika merupakan metode untuk mengetahui hubungan antara faktor-faktor atau variabel-variabel yang diamati. Penggunaan korelasi sering sekali dikenal sebagai metode untuk melihat adanya kekuatan, bentuk arah, dan besarnya hubungan antar variabel, serta mengetahui erat atau tidaknya hubungan antar variabel. Dalam matematika, korelasi disimbolkan dengan ρ (rho) sebagai populasi atau r sebagai sampel.
Metode yang paling dasar digunakan untuk mengetahui hubungan antar variabel yaitu korelasi linear sederhana atau korelasi Pearson product moment. Korelasi linear sederhana merupakan metode korelasi yang digunakan untuk mengukur arah dan kekuatan hubungan 2 variabel. Rumus umum korelasi linear sederhana atau korelasi pearson product moment didefinisikan sebagai berikut:
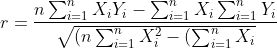^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}})
dengan n merupakan banyaknya sampel atau observasi pada data,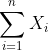 dan
dan 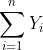 merupakan jumlah nilai dari faktor/variabel X dan Y dari observasi/sampel ke-1 hingga ke-n.
merupakan jumlah nilai dari faktor/variabel X dan Y dari observasi/sampel ke-1 hingga ke-n.
Koefisien korelasi berada diantara -1 hingga 1. Koefisien korelasi menandakan arah serta kekuatan hubungan antar variabel. Arah korelasi antar variabel ditunjukkan dari tanda pada hasil koefisien korelasi. Apabila koefisien korelasi bertanda positif (+), maka:
-Apabila nilai variabel ditingkatkan, maka akan meningkatkan nilai variabel yang lain
-Apabila nilai variabel diturunkan, maka akan menurunkan nilai variabel yang lain
Apabila koefisien korelasi bertanda negatif (-), maka:
-Apabila nilai variabel ditingkatkan, maka akan menurunkan nilai variabel yang lain
-Apabila nilai variabel diturunkan, maka akan meningkatkan nilai variabel yang lain
Koefisien korelasi bertanda positif (+) menunjukkan arah hubungan yang searah, sementara koefisien korelasi bertanda negatif (-) menunjukkan arah hubungan yang berlawanan. Selain itu kekuatan korelasi antara variabel ditunjukkan dari rentang nilai pada hasil koefisien korelasi, baik positif maupun negatif. Berikut ini merupakan kekuatan korelasi antar variabel dari selang-selang tertentu menurut Walpole (2004):
Pada umumnya, korelasi berasal dari dua kata, yaitu "Co-" dan "Relation". Kata "Co-" menunjukkan bersama, bergabung, sepasang, atau derajat/tingkat yang sama. Dan "relation" menunjukkan relasi, dampak atau hubungan. Jadi secara umum, definisi korelasi menurut penggunaan statistika merupakan metode untuk mengetahui hubungan antara faktor-faktor atau variabel-variabel yang diamati. Penggunaan korelasi sering sekali dikenal sebagai metode untuk melihat adanya kekuatan, bentuk arah, dan besarnya hubungan antar variabel, serta mengetahui erat atau tidaknya hubungan antar variabel. Dalam matematika, korelasi disimbolkan dengan ρ (rho) sebagai populasi atau r sebagai sampel.
Metode yang paling dasar digunakan untuk mengetahui hubungan antar variabel yaitu korelasi linear sederhana atau korelasi Pearson product moment. Korelasi linear sederhana merupakan metode korelasi yang digunakan untuk mengukur arah dan kekuatan hubungan 2 variabel. Rumus umum korelasi linear sederhana atau korelasi pearson product moment didefinisikan sebagai berikut:
dengan n merupakan banyaknya sampel atau observasi pada data,
Koefisien korelasi berada diantara -1 hingga 1. Koefisien korelasi menandakan arah serta kekuatan hubungan antar variabel. Arah korelasi antar variabel ditunjukkan dari tanda pada hasil koefisien korelasi. Apabila koefisien korelasi bertanda positif (+), maka:
-Apabila nilai variabel ditingkatkan, maka akan meningkatkan nilai variabel yang lain
-Apabila nilai variabel diturunkan, maka akan menurunkan nilai variabel yang lain
Apabila koefisien korelasi bertanda negatif (-), maka:
-Apabila nilai variabel ditingkatkan, maka akan menurunkan nilai variabel yang lain
-Apabila nilai variabel diturunkan, maka akan meningkatkan nilai variabel yang lain
Koefisien korelasi bertanda positif (+) menunjukkan arah hubungan yang searah, sementara koefisien korelasi bertanda negatif (-) menunjukkan arah hubungan yang berlawanan. Selain itu kekuatan korelasi antara variabel ditunjukkan dari rentang nilai pada hasil koefisien korelasi, baik positif maupun negatif. Berikut ini merupakan kekuatan korelasi antar variabel dari selang-selang tertentu menurut Walpole (2004):
| No | Selang Koefisien Korelasi | Kekuatan Hubungan |
|---|---|---|
| 1 | 0.0 ≤ r < 0.2 | Sangat Lemah |
Tidak ada hubungan (|r| = 0) 2 0.2 ≤ r < 0.4 Lemah 3 0.4 ≤ r < 0.6 Sedang/Biasa 4 0.6 ≤ r < 0.8 Kuat 5 0.8 ≤ r < 1.0 Sangat Kuat
Sempurna (|r| = 1)
Dalam scatter plot, arah dan kekuatan hubungan antar variabel dapat digambarkan sebagai berikut:
Berdasarkan hasil diatas menunjukkan arah korelasi (kiri) dan kekuatan korelasi (kanan) berdasarkan scatter plot (plot pencaran). Arah korelasi yang positif (positive correlation) ditunjukkan dengan kumpulan titik-titik yang membentuk pola linear naik ke atas kanan. Arah korelasi yang negatif (negative correlation) ditunjukkan dengan kumpulan titik-titik yang membentuk pola linear turun ke ke bawah kanan. Sementara tidak ada korelasi (no correlation) ditunjukkan dengan korelasi yang membentuk selain dua pola linear tersebut, seperti pola vertikal, pola horizontal, maupun pola yang lainnya. Kekuatan korelasi yang kuat (strong correlation) ditunjukkan dengan sekumpulan titik-titik yang saling berdekatan satu sama lain, sementara kekuatan korelasi yang lemah (weak correlation) ditunjukkan dengan sekumpulan titik-titik yang saling berjauhan satu sama lainnya.
Agar paham bagaimana cara menghitung korelasi antar variabel, berikut ini merupakan data mengenai permintaan suatu komoditi (satuan) dan harga rata-rata komoditi (satuan). Permintaan suatu komoditi didefinisikan sebagai variabel X dan harga rata-rata komoditi didefinisikan sebagai variabel Y. Data berikut sudah dihitung nilai X2, Y2, dan XY serta jumlah dari semua variabelnya.
Berdasarkan hasil tabel diatas diperoleh nilai:
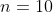
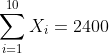
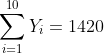
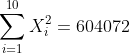
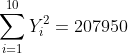
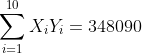
Nilai-nilai tersebut dimasukkan ke formula korelasi Pearson product moment (korelasi linear sederhana) sebagai berikut:
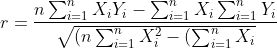^{2})(n\sum_{i=1}^{n}Y_{i}^{2}-(\sum_{i=1}^{n}Y_{i})^{2})}})
-(2400)(1240)}{\sqrt{(10(604072)-(2400)^2)(10(207950)-(1420)^2)}})
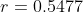
Berdasarkan hasil perhitungan korelasi Pearson product moment diatas menunjukkan bahwa koefisien Korelasi antara permintaan suatu komoditi (X) dengan harga rata-rata komoditi (Y) sebesar 0.5477 dengan hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang menengah sehingga apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi. Sebaliknya, apabila dikurangkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi.
Ilustrasi lain dengan kasus yang sama (Kasus hubungan antara permintaan suatu komoditi (X) dengan harga rata-rata komoditi (Y) dengan nilai data yang berbeda, setelah dilakukan perhitungan hasil koefisien korelasinya menunjukkan nilai -0.8096, bagaimana interpretasinya? Hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang sangat kuat sehingga apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi. Sebaliknya, apabila dikurangkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi.
Demikian pengertian dan perhitungan korelasi Pearson product moment atau korelasi linear sederhana yang bisa saya sampaikan dalam blog ini. Semoga bermanfaat.
Sempurna (|r| = 1)
Dalam scatter plot, arah dan kekuatan hubungan antar variabel dapat digambarkan sebagai berikut:
 |
| Gambaran umum arah dan kekuatan korelasi berdasarkan Scatter Plot |
Agar paham bagaimana cara menghitung korelasi antar variabel, berikut ini merupakan data mengenai permintaan suatu komoditi (satuan) dan harga rata-rata komoditi (satuan). Permintaan suatu komoditi didefinisikan sebagai variabel X dan harga rata-rata komoditi didefinisikan sebagai variabel Y. Data berikut sudah dihitung nilai X2, Y2, dan XY serta jumlah dari semua variabelnya.
| No | X (Permintaan Suatu Komoditi) | Y (Rata-Rata Harga Komoditi) | X^2 | Y^2 | XY |
|---|---|---|---|---|---|
| 1 | 178 | 105 | 31684 | 11025 | 18690 |
| 2 | 224 | 105 | 50176 | 11025 | 23520 |
| 3 | 160 | 130 | 25600 | 16900 | 20800 |
| 4 | 315 | 130 | 99225 | 16900 | 40950 |
| 5 | 229 | 130 | 52441 | 16900 | 29770 |
| 6 | 250 | 150 | 62500 | 22500 | 37500 |
| 7 | 181 | 150 | 32761 | 22500 | 27150 |
| 8 | 306 | 170 | 93636 | 28900 | 52020 |
| 9 | 257 | 170 | 66049 | 28900 | 43690 |
| 10 | 300 | 180 | 90000 | 32400 | 54000 |
| Jumlah | 2400 | 1420 | 604072 | 207950 | 348090 |
Berdasarkan hasil tabel diatas diperoleh nilai:
Nilai-nilai tersebut dimasukkan ke formula korelasi Pearson product moment (korelasi linear sederhana) sebagai berikut:
Berdasarkan hasil perhitungan korelasi Pearson product moment diatas menunjukkan bahwa koefisien Korelasi antara permintaan suatu komoditi (X) dengan harga rata-rata komoditi (Y) sebesar 0.5477 dengan hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang menengah sehingga apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi. Sebaliknya, apabila dikurangkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi.
Ilustrasi lain dengan kasus yang sama (Kasus hubungan antara permintaan suatu komoditi (X) dengan harga rata-rata komoditi (Y) dengan nilai data yang berbeda, setelah dilakukan perhitungan hasil koefisien korelasinya menunjukkan nilai -0.8096, bagaimana interpretasinya? Hubungan antara permintaan suatu komoditi dengan harga rata-rata komoditi memiliki tingkat hubungan yang sangat kuat sehingga apabila ditambahkan permintaan suatu komoditi maka akan mempengaruhi penurunan harga rata-rata suatu komoditi. Sebaliknya, apabila dikurangkan permintaan suatu komoditi maka akan mempengaruhi peningkatan harga rata-rata suatu komoditi.
Demikian pengertian dan perhitungan korelasi Pearson product moment atau korelasi linear sederhana yang bisa saya sampaikan dalam blog ini. Semoga bermanfaat.
Langganan:
Komentar (Atom)